La rumeur coure encore de nos jours comme quoi la division par zéro est impossible. Parfois, les gens en parlent comme si l’espace-temps se fracturerait si on divisait quoi que ce soit par 0. Si on essaye à la calculatrice d’opérer une telle division, un code d’erreur nous est retourné : même la machine ne nous donne pas une réponse. Est-ce que c’est parce qu’effectivement il n’y a pas de solution possible? Lorsqu’on s’attarde un peu, il est facile d’en trouver plusieurs! Pourtant la calculatrice me dit que c’est impossible, mais ce code d’erreur est préprogrammé : la calculatrice n’essaie même pas d’y répondre. La division par zéro est un exemple parfait de l’admission des contradictions dans le cosmos et la réponse de ma calculatrice n’est qu’idéologie.

Le précédent article a conclu que le langage et la nature permettent l’usage des contradictions et que le système de la logique classique se fourvoyait sur la validité des contradictions. Dans cet article, nous couvrirons le langage même de la nature : les mathématiques. Nous verrons comment la division par zéro est exemplaire dans sa réponse à la question de la validité de l’idéologie de la non-contradiction.

Par exemple, 0/0 est une division qui comporte, dans l’absolu, cinq solutions qui se contredisent toutes et de toutes les manières possibles sans pour autant qu’il soit possible différencier les réponses sur la valeur de leur validité, et dans l’application pratique, elle comporte plus qu’une infinité de réponses possibles. Le lecteur atteindra lors de sa lecture, l’hyperespace de la contradiction et ne pourra plus, une fois lecture terminée, douter de la validité des contradictions.

Les équations à réponses multiples ne sont pas une chose rare dans les mathématiques, pourtant la division par zéro fait exception. C’est une des seules opérations dont la multiplicité des réponses n’est pas tolérée, si bien qu’on irait jusqu’à prétendre qu’il soit impossible de diviser par 0 et considérer le dossier clos : mais accepter cette réponse devrait aussi mener à renoncer la division par 1. Pourquoi peut-on additionner, soustraire, multiplier tous les nombres, mais que la division, elle, aurait pour limites le 0 ?

La gêne du x/0

Il y existe quelques équations en mathématiques ayant pour particularité d’avoir plusieurs réponses possibles. Prenons l’exemple du 2x=1. Pour résoudre 2x=1, nous devons accepter de vivre avec deux possibilités concurrentes, aux polarités contraires. En effet si 2x = 1, alors x = 1 ou -1. Il est impossible avec l’information disponible de déterminer si x a pour valeur 1 ou -1.

Les mathématiciens peuvent vivre dans un monde où plus d’une possible réponse existe pour une même équation, même si les réponses sont l’opposée l’une de l’autre. Après tout, il n’y a pas de contradiction car le mathématicien a confiance que seule une des réponses est la bonne et qu’advenant le cas où le problème est rencontré dans la réalité, il pourra trancher sur la valeur définitive de x.

Disons que si dans l’absolu, on ne peut donner de réponse définitive à 2x = 1, dans la pratique, le contexte peut nous informer de la réponse finale : il est impossible de trouver un deux-par-quatre mesurant -1 mètre à la quincaillerie, alors, dans ce cas, le mathématicien déterminera qu’en toute vraisemblance la réponse est 1.

On peut tolérer l’incertitude dans l’absolu en mathématique si nous avons confiance qu’une réponse certaine pourra ou pourrait être donnée dans un cas concret. Dans ce cas, ces équations peuvent avoir plusieurs réponses possibles, même si opposées, et on ne dira pourtant pas ces réponses contradictoires, mais plutôt concurrentes. Elles sont en concurrence, mais nous savons que nous n’aurons qu’une solution gagnante.

Avec la division par 0, les choses se compliquent. Si dans l’absolu, nous avons plusieurs réponses, celles-ci n’y sont pas concurrentes : elles se valent toutes autant les unes que les autres, et il est impossible de recourir à un usage pratique pour soulager l’incertitude, car l’usage pratique nous donne une autre réponse que les calculs dans l’absolu. Voyons voir…

/0 en théorie et en pratique

Dans l’absolu, diviser par zéro comporte quelques solutions qui soient plutôt facile à démontrer. Une manière de répondre à l’équation 1/0=x et donner une valeur à x, est de procéder en déduisant la valeur dans la série de dénominateurs.

1/100 = 0.01
1/10 = 0.1
1/5 = 0.2
1/2 = 0.5
1/1 = 1
1/0.1 = 10
1/0.01 = 100
1/0.001 = 1000
…
1/0=∞

Plus le dénominateur d’une fraction est grand, plus le nombre est petit. Plus le dénominateur est petit, plus le nombre est grand. En théorie, nous aurions 0 en divisant 1 par ∞, et en divisant 1 par 0, ∞. Ceci est simplement la suite logique de l’ensemble de toutes les fractions.

Mais nous pourrons aussi reconnaître que, si nous plaçons toutes les valeurs de dénominateurs possible dans un plan cartésien, nous avons là une fonction exponentielle. Il y aurait donc une asymptote. Rappel au lecteur : l’asymptote est la valeur qui ne sera jamais atteinte par notre courbe, en pratique, car pour cela, il faudrait pouvoir se rendre à l’infini. En pratique, la limite existe. En théorie, elle n’existe pas. Donc nous voyons ici que la théorie nous dit que la réponse est ∞, mais que la pratique nous donne plutôt la réponse N/A (non applicable)…

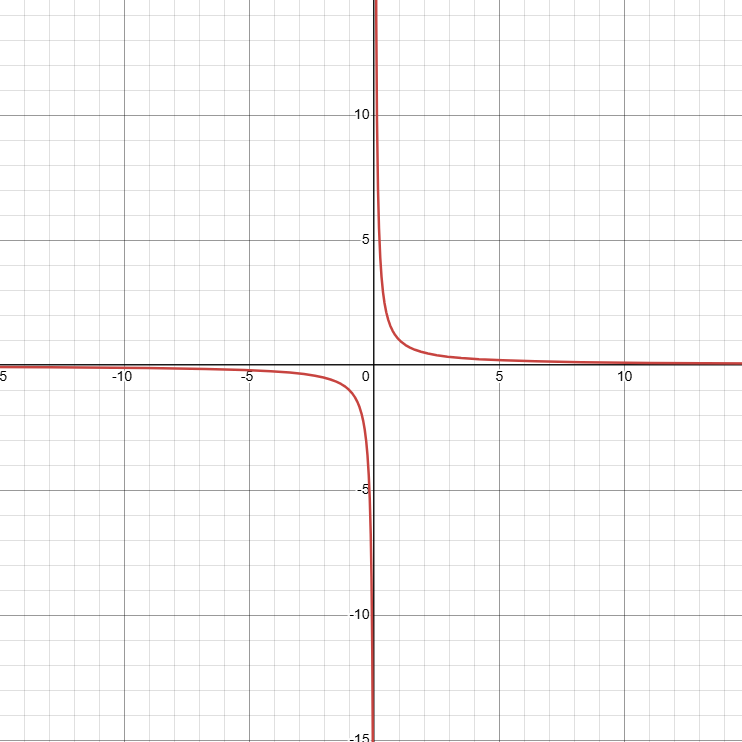
Il y a donc ici deux réponses qui soient contradictoires. Par deux méthodes fût démontré qu’en théorie la division par zéro a pour résultat infini : celle de la série des dénominateurs, et sa mise en graphique avec les asymptotes. Mais cette dernière a aussi souligné que la pratique donne une réponse toute autre venant contredire la théorie à un niveau fondamental. Il est impossible de plus se contredire que ceci. La théorie nous donne une réponse, alors que la pratique dit plutôt qu’il n’y a pas de réponse

%=? …

Et ça devient encore plus étrange lorsqu’on arrive à %. (Oui, je sais, ce symbole signifie le pourcentage. Mais objectivement, % représente la fraction 0/0 tout comme ½ représente 1/2.) % a encore plus de solutions que x/0. Il y a en fait 4 solutions en théorie, ainsi qu’une infinité de solutions en pratique.

Voyons voir…

La première solution de placer les dénominateurs en série fonctionne encore pour ce cas. Donc une première réponse est ∞.

Une seconde solution est de procéder de la même façon, mais avec les nominateurs. Plus le nominateur est petit, plus le nombre est petit.

10/2 = 5
5/2 = 2.5
3/2 = 1.5
½ = 0.5
0.01/2 = 0.005
…
0/2 = 0

En théorie, nous aurions la réponse infiniment plus petite que la première. Comme la série va vers un nombre toujours plus petit à mesure que diminue le nominateur, il serait logique qu’à 0, ce soit le plus petit nombre possible, 0. Mais lorsqu’on divise 0 par 0, – ∞ serait aussi une réponse possible. Puisque +0 et -0 sont égales l’une à l’autre, -0/0 donnerait – ∞.

Une troisième solution est la réponse à l’équation 0/x. Pour tout les nombres ayant un nominateur de 0, nous avons que la réponse soit elle aussi de 0… Pourquoi % serait-il une exception à cette règle? Ne voyant de raison, nous avons donc que la réponse soit aussi 0.

La quatrième solution est que nous avons que la solution de x/x, pour toute valeur de x, est 1. 1/1=1, 2/2=1, 18/18=1, 1000/1000=1, -1/-1=1, -1000/-1000/1. Pourquoi % serait-il une exception? Encore une fois, ne voyant de raison, nous avons donc que la réponse soit aussi 1.

Nos réponses possibles sont ∞, – ∞, 0 et 1.

On va couper le gâteau

Finalement, une cinquième solution consiste à se questionner sur ce que c’est qu’une division. Comment pouvons-nous diviser quoi que ce soit par 0. Je peux couper un gâteau en 8. Je peux partager une somme d’argent en deux parties égales. Mais comment couper un gâteau en 0? Voici pourquoi les mathématiciens disent que de diviser par zéro est impossible.

Suivant cette logique, si diviser par zéro est impossible alors diviser par un le serait tout autant. Comment couper un gâteau en un? C’est un non-sens. N’importe quelle coupe qu’on fasse sépare le gâteau et on échoue à la tâche de couper le gâteau en un. Certains diront qu’il faut simplement ne pas couper et que voici voilà on l’aurait divisé par un. Mais si on n’a pas coupé quoi que ce soit, comment dire qu’on a séparé le gâteau? Nous n’avons simplement pas opéré de division. Pour diviser en un, il faut ne pas diviser : donc la division en un est aussi impossible que la division par zéro. Suivant cette logique, n’importe quelle opération par zéro serait impossible, comment ajouter ou soustraire rien? Comment multiplier par rien?

C’est que la division ne couvre pas uniquement la découpe d’un gâteau et les proportions ou la géométrie sont plus utile au problème de découpage du gâteau que l’arithmétique de la division. Après tout, qui sort un papier et un crayon pour faire une division avant de commencer à couper un gâteau? Formuler la question de la division ainsi, c’est se méprendre sur l’outil de la division. La division n’est pas un outil servant essentiellement à séparer ou à répartir, c’est un outil qui nous dit comment stocker un contenu ou remplir des contenants.

Les Tupperwares de la division

Nous pouvons formuler le problème ainsi : une division comporte deux parties, un nominateur et un dénominateur. Nous pouvons les voir comme un contenu et un contenant. Diviser quoi que ce soit par quoi que ce soit revient à se demander combien de contenants pouvant contenir une quantité y de contenu ai-je besoin pour stocker une quantité x contenu. Ou encore, combien de contenants avec une capacité y de quelque chose puis-je remplir avec une quantité x de cette même chose. Nous verrons que la solution à ces deux problèmes mène encore à des réponses contradictoires.

En un premier temps, diviser par zéro revient alors à se demander combien de contenants sont nécessaires afin de stocker x de quelque chose (contenu) dans des contenants ayant la capacité de contenir 0 de cette même chose. On ne peut simplement pas répondre à cette question. La réponse est : c’est impossible. C’est cette formulation que retiennent les mathématiciens.

Mais, en un second temps, diviser par zéro revient aussi à se demander combien de contenants n’ayant aucune capacité puis-je remplir avec une quantité x? La réponse est n’importe quel nombre de 0 à infini inclusivement. Peu importe la raison pour laquelle les contenants ont une capacité nulle, soit parce qu’ils sont déjà pleins, soit parce qu’ils sont trop petits pour contenir une unité d’un objet non séparable, nous avons aussi la possibilité donc de tous les remplir, même si je n’ai aucune quantité de contenu.

Par exemple : combien de télévisions puis-je stocker dans une boîte trop petite pour une télévision? Une réponse en bas de 1 signifie simplement que je dois couper une télévision afin de résoudre mon problème et donc assumer une perte, ce qui n’a plus de sens pour un fabricant cherchant à vendre ses télévisions. Peu importe le nombre de boîte trop petite que j’ai, je peux les considérer toutes déjà remplies. Je ne peux pas stocker de télévision et toutes les boîtes sont remplies.

Les réponses sont N/A et un nombre choisi arbitrairement ou au hasard, de 0 à infini inclusivement. Donc nous avons plus d’une infinité de réponses possibles.

Et on ne peut pas dire qu’une des réponses soit invalide. Dans les deux cas on a divisé par zéro de façon légitime. Si l’objectif est de stocker une quantité quelconque, la tâche est impossible. Si l’objectif est de remplir des contenants trop petits ou déjà à pleine capacité, la tâche est déjà faite et je peux dire le nombre que je veux. Le cas de la division par zéro incarne le libertarisme dans les mathématiques.

Conclusion

Nous nous retrouvons après toute cette péripétie avec la situation suivante : dans le monde absolu des mathématiques théoriques, diviser par zéro a deux solutions contradictoires sans être nécessairement concurrentes, et dans la pratique, diviser par zéro a une infinité de solutions dans certains cas et une impossibilité de solutionner dans certains autres cas. Il n’est donc pas impossible de diviser par zéro. C’est un mythe. La division par zéro a simplement une infinité de solutions possibles dont l’impossibilité de résoudre le problème. L’impossibilité de résoudre le problème ne signifie pas qu’il soit impossible de résoudre l’équation.

Il faut pour cela reconnaître non seulement que le langage de la nature fonctionne avec des contradictions, mais aussi que l’auto-référentialité est autorisée. Le zéro ne désigne pas quelque chose, mais une absence. Dans la définition de ce qu’est un nombre, le zéro joue un rôle fondamental : c’est un faisant un ensemble contenant zéro de quoi que ce soit, du vide, que nous obtenons un zéro, mais si on fait un ensemble contenant ce zéro, nous obtenons la définition du nombre 1. 1={0}. 0={ }* *ensemble vide, un vide se défini comme une quantité 0 de quoi que ce soit… Donc la définition de 0 est circulaire, sa forme aussi d’ailleurs.

L’autoréférentialité est aussi ce qu’autorise la réponse à %. On peut donner la réponse que l’on veut et se sera une bonne réponse, simplement car c’est la réponse qu’on a donnée. Lorsqu’on demande à quelqu’un de nous donner un nombre au hasard, il fait en fait une division de zéro par zéro.

% serait-il la garantie mathématique nous indiquant que la liberté est une propriété de la nature et qu’elle est inscrite dans son langage? La réponse qu’on donne à % en dit long sur la personne qui donne la réponse : s’il choisi le N/A, c’est peut-être une personne qui renonce à la liberté que lui donne la nature. S’il choisi un nombre quelconque ou infini, c’est une personne qui en jouit. Et s’il donne toute ces réponses, c’est probablement un sage qui vous répond.